Tài liệu Giáo viên
Lớp 2Lớp 2 - liên kết tri thức
Lớp 2 - Chân trời sáng sủa tạo
Lớp 2 - Cánh diều
Tài liệu Giáo viên
Lớp 3Lớp 3 - liên kết tri thức
Lớp 3 - Chân trời sáng tạo
Lớp 3 - Cánh diều
Tài liệu Giáo viên
Tài liệu Giáo viên
Lớp 4Lớp 4 - liên kết tri thức
Lớp 4 - Chân trời sáng sủa tạo
Lớp 4 - Cánh diều
Tiếng Anh lớp 4
Tài liệu Giáo viên
Lớp 5Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
Lớp 6Lớp 6 - liên kết tri thức
Lớp 6 - Chân trời sáng tạo
Lớp 6 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 7Lớp 7 - kết nối tri thức
Lớp 7 - Chân trời sáng tạo
Lớp 7 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 8Lớp 8 - liên kết tri thức
Lớp 8 - Chân trời sáng tạo
Lớp 8 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 9Sách giáo khoa
Sách/Vở bài xích tập
Tài liệu Giáo viên
Lớp 10Lớp 10 - liên kết tri thức
Lớp 10 - Chân trời sáng sủa tạo
Lớp 10 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 11Lớp 11 - liên kết tri thức
Lớp 11 - Chân trời sáng tạo
Lớp 11 - Cánh diều
Tiếng Anh
Tài liệu Giáo viên
Lớp 12Sách giáo khoa
Sách/Vở bài bác tập
Tài liệu Giáo viên
cô giáoLớp 1
Lớp 2
Lớp 3
Lớp 4
Lớp 5
Lớp 6
Lớp 7
Lớp 8
Lớp 9
Lớp 10
Lớp 11
Lớp 12

Bộ đề thi Toán lớp 7Bộ đề thi Toán lớp 7 - liên kết tri thức
Bộ đề thi Toán lớp 7 - Cánh diều
Bộ đề thi Toán lớp 7 - Chân trời sáng sủa tạo
Đề kiểm tra 1 tiết Toán 7 Chương 1 Hình học gồm đáp án, rất hay (4 đề)
Trang trước
Trang sau
Đề kiểm tra 1 huyết Toán 7 Chương 1 Hình học có đáp án, rất hay (4 đề)
Để ôn luyện cùng làm giỏi các bài xích kiểm tra Toán lớp 7, dưới đó là Top 4 Đề kiểm tra 1 ngày tiết Toán 7 Chương 1 Hình học có đáp án, cực hay. Hi vọng bộ đề chất vấn này để giúp bạn ôn luyện & đạt điểm cao trong những bài soát sổ môn Toán lớp 7.
Bạn đang xem: Những bài toán hình hay lớp 7 có đáp án
Phòng giáo dục đào tạo và Đào tạo .....
Đề bình chọn 1 huyết Chương 1 Hình học
Môn: Toán lớp 7
Thời gian có tác dụng bài: 45 phút
(Trắc nghiệm + từ bỏ luận - Đề 1)
I. Phần trắc nghiệm khách quan: (3 điểm).
Trong từng câu bên dưới đây, nên lựa chọn phương án trả lời đúng:
Câu 1: có số đo bởi 70o. Góc đối đỉnh với gồm số đo là:
A. 90o
B. 140o
C. 70o
D. 150o
Câu 2: hai đường thẳng xx" và yy" cắt nhau tại điểm O tạo nên thành 4 góc. Tổng số những cặp góc đối đỉnh (không kể góc bẹt) là:
A. 3 cặp
B. 6 cặp
C. 9 cặp
D. 2 cặp
Câu 3: Đường trung trực của đoạn thẳng AB là:
A. Đường thẳng vuông góc cùng với đoạn AB
B. Đường thẳng đi qua trung điểm của AB
C . Đường trực tiếp vuông góc với AB tại trung điểm của AB
D. Đường trực tiếp vuông góc với AB trên A.
Câu 4: tiên đề Ơclít được vạc biểu:
“Qua một điểm M nằm ở ngoài đường thẳng a ....”
A. Có duy nhất một đường thẳng đi qua M và tuy vậy song với a.
B. Có hai tuyến phố thẳng tuy vậy song với a.
C. Có tối thiểu một đường thẳng tuy nhiên song cùng với a.
D. Tất cả vô số con đường thẳng tuy vậy song với a.
Câu 5: trường hợp c ⊥ a và b ⊥ a thì:
A. A // b
B. B // c
C. A ⊥ b
D. C ⊥ b
Câu 6: vào các khẳng định sau, khẳng định nào sai?
A. Trường hợp a // c cùng b // c thì a // b
B. Nếu a ⊥ c và b ⊥ c thì a // b
C. Giả dụ a ⊥ c với b ⊥ c thì a ⊥ b
D. Ví như a ⊥ c với b // c thì a ⊥ b
II. Phần từ bỏ luận: (7 điểm)
Câu 1: (2 điểm) phát biểu định lý diễn tả bằng mẫu vẽ sau. Viết mang thiết và tóm lại của định lý đó bằng ký hiệu.
Câu 2: (2 điểm)Vẽ hai tuyến đường thẳng xx’ với yy’ giảm nhau tại O làm thế nào cho
Oy’; x’Oy’; x’Oy?
Câu 3: (2 điểm) đến hình vẽ. Biết a // b ;
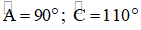
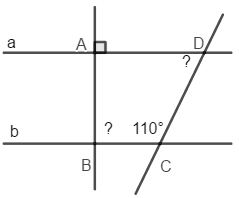
Câu 4: (1 điểm) đến hình vẽ, biết
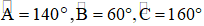
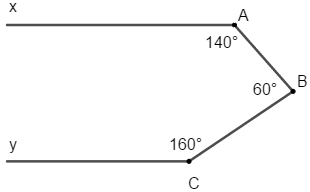
Đáp án và khuyên bảo làm bài
I. Phần trắc nghiệm khách hàng quan: (3 điểm, mỗi câu đúng được 0,5 điểm).
| Câu | 1 | 2 | 3 | 4 | 5 | 6 |
| Đáp án | C | D | C | A | B | C |
Câu 1:
Góc đối đỉnh với gồm số đo chính bằng và bởi 70o (Hai góc đối đỉnh thì bằng nhau).
Chọn giải đáp C
Câu 2:
Theo định nghĩa, hai đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh.
Chọn câu trả lời D.
Câu 3:
Đường trung trực của đoạn trực tiếp AB là mặt đường thẳng vuông góc cùng với AB tại trung điểm của AB.
Chọn đáp án C.
Câu 4:
Tiên đề Ơclít được phạt biểu:
“Qua một điểm M nằm ở ngoài đường thẳng a có duy tốt nhất một mặt đường thẳng đi qua M và tuy nhiên song với a”.
Chọn lời giải A.
Câu 5:
Ta có:
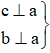
Arr; b // c
Chọn lời giải B
Câu 6:
+ giả dụ a // c và b // c thì a // b đúng (theo tính chất ba đường thẳng song song)
+ nếu a ⊥ c cùng b ⊥ c thì a // b đúng (theo quan hệ tình dục giữa tính vuông góc và tính tuy vậy song)
+ ví như a ⊥ c và b ⊥ c thì a ⊥ b sai, vì chưng a // b
+ giả dụ a ⊥ c và b // c thì a ⊥ b là đúng (theo quan hệ tình dục giữa tính vuông góc cùng tính tuy nhiên song)
Chọn lời giải C.
II. Phần tự luận: (7 điểm).
Câu 1:
Định lí: hai tuyến đường thẳng riêng biệt cùng vuông góc cùng với một con đường thẳng thứ bố thì chúng tuy vậy song với nhau. (1 điểm)
GT | a, b phân biệt a ⊥ c, b ⊥ c |
KL | a // b |
(1điểm)
Câu 2:
Vẽ hình đúng (0,5 điểm)
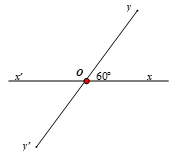
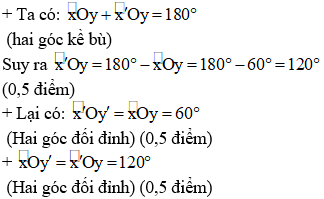
Câu 3:
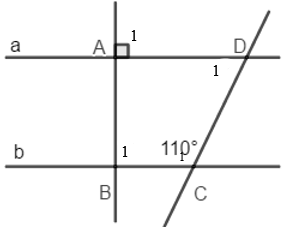
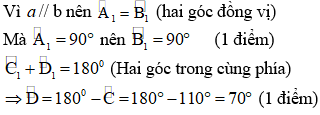
Câu 4:
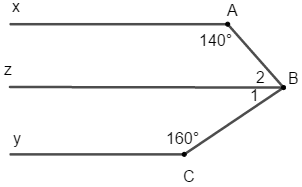
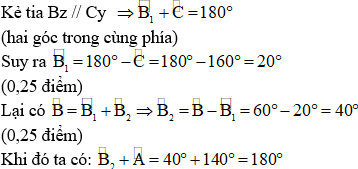
Mà hai góc này ở đoạn trong thuộc phía
Do đó Ax // Bz
Mà Bz // Cy
Vậy Ax // Cy (đpcm). (0,5 điểm)
Phòng giáo dục và Đào sản xuất .....
Đề khám nghiệm 1 huyết Chương 1 Hình học
Môn: Toán lớp 7
Thời gian làm bài: 45 phút
(Trắc nghiệm + từ bỏ luận - Đề 2)
I . Phần trắc nghiệm khách hàng quan: (3đ)
Trong mỗi câu dưới đây, nên chọn lựa phương án trả lời đúng:
Câu 1: hai góc đối đỉnh thì
A . Bù nhau.
B. Phụ nhau.
C. Bởi nhau.
D. Cùng bởi 90o.
Câu 2: hai tuyến phố thẳng cắt nhau chế tác thành từng nào cặp góc đối đỉnh.
A. 1.
B. 2.
C. 3.
D. 4.
Câu 3: hai đường thẳng vuông góc là hai đường thẳng cắt nhau và trong số góc sinh sản thành bao gồm
A. 0 góc vuông.
B. 1 góc vuông.
C . 2 góc vuông.
D. 3 góc vuông.
Câu 4: Đường trực tiếp xy là trung trực của đoạn thẳng MN khi
A. Xy trải qua điểm I của MN.
B. Xy ⊥ MN.
C. Xy ⊥ MN tại I và IM = IN.
D. Xy // MN và IM = IN.
Câu 5: qua 1 điểm ở đi ngoài đường thẳng mang lại trước, ta vẽ được từng nào đường thẳng song song với con đường thẳng cho trước.
A. 1.
B. 2.
C. 3.
D. 4.
Câu 6: Số điểm bình thường của hai tuyến phố thẳng tuy vậy song là
A. 0
B. 1
C. 2
D. 3.
Câu 7: trường hợp a // b cùng a // c thì
A . B // c.
B . A ⊥ c.
C b ⊥ c.
D. B ≡ c.
Câu 8: ví như a ⊥ b với a // c thì
A. A // b.
B. B // c.
C. A ⊥ c.
D. B ⊥ c.
Câu 9: nếu như a ⊥ b cùng b ⊥ c thì
A. A ⊥ c.
B. A // c.
C. A // b.
D. C // b.
Câu 10: bên trên hình dưới, cặp góc so le trong là
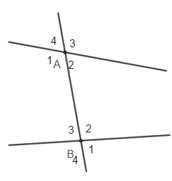
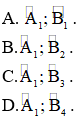
Câu 11: trường hợp một mặt đường thẳng cắt hai tuyến phố thẳng tuy nhiên song thì
A. Cặp góc đồng vị bù nhau.
B. Cặp góc trong cùng phía bằng nhau.
C. Cặp góc so le trong bằng nhau.
D. Cặp góc so le ko kể bù nhau.
Câu 12: Để chứng minh "Hai góc đối đỉnh thì bởi nhau” với công việc lập luận sau:
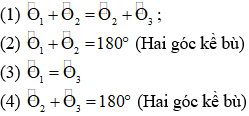
Sắp xếp lại quá trình lập luận nhằm được chứng tỏ đúng là
A.(1),(2) → (3) → (4).
B.(1),(3) → (2) → (4).
C.(2),(4) → (1) → (3).
D.(3),(2) → (1) → (4).
II. Phần tự luận: (7,0 điểm)
Câu 1: (2,0 điểm) mang đến đoạn trực tiếp AB = 5 cm. Vẽ con đường trung trực của đoạn thẳng AB, nói rõ cách vẽ.
Câu 2: (3,0 điểm)
Cho hình bên: Biết a // b. 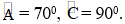 a) Nêu giả thiết, kết luận b)Tính số đo của  | 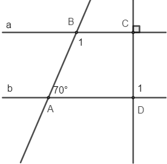 |
Câu 3: (2,0 điểm) đến hình sau:
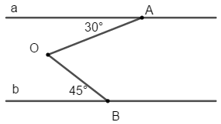
Biết a // b ;
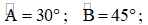
Tính góc AOB ?
Đáp án và hướng dẫn làm bài
I. Phần trắc nghiệm khách quan: (3 điểm, từng câu đúng được 0,25 điểm).
| Câu | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Đáp án | C | B | B | C | A | A | A | D | B | B | C | C |
Câu 1:
Hai góc đối đỉnh thì bởi nhau.
Chọn lời giải C.
Câu 2:
Theo lý thuyết, hai đường thẳng giảm nhau tạo thành thành 2 cặp góc đối đỉnh.
Chọn giải đáp B.
Câu 3:
Theo định nghĩa: hai tuyến phố thẳng vuông góc là hai đường thẳng cắt nhau và trong số góc chế tạo ra thành có một góc vuông.
Chọn giải đáp B.
Câu 4:
Đường thẳng vuông góc với một quãng thẳng tại trung điểm của chính nó được điện thoại tư vấn là mặt đường trung trực của đoạn trực tiếp ấy.
Do đó đường thẳng xy là trung trực của đoạn thẳng MN lúc xy ⊥ MN trên I với IM = IN.
Chọn lời giải C.
Câu 5:
Theo định đề Ơ - clít: "Qua một điểm ở ngoài đường thẳng đến trước, chỉ tất cả một mặt đường thẳng tuy nhiên song với mặt đường thẳng cho trước."
Chọn câu trả lời A.
Câu 6:
Hai mặt đường thẳng tuy vậy song thì không có điểm chung.
Chọn đáp án A.
Câu 7:
Theo dục tình giữa ba đường thẳng song song
Ta có: a // b và a // c, suy ra b // c.
Chọn giải đáp A.
Câu 8:
Ta có:
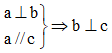
Chọn câu trả lời D.
Câu 9:
Ta có:
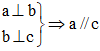
Chọn lời giải B.
Câu 10:
Góc A1 so le vào với góc B2.
Chọn đáp án B.
Câu 11:
Nếu một mặt đường thẳng cắt hai đường thẳng song song thì:
+ Cặp góc đồng vị bởi nhau.
+ Cặp góc trong cùng phía bù nhau.
+ Cặp góc so le trong bởi nhau.
+ Cặp góc so le ngoài bằng nhau.
Chọn đáp án C.
Câu 12:
Ta minh chứng như sau:
Hai mặt đường thẳng xx" với yy" giảm nhau tại O.
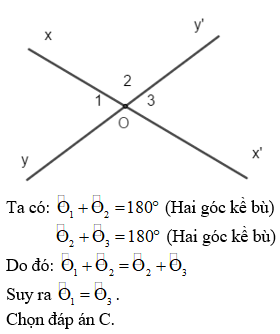
II. Phần trường đoản cú luận (7 điểm)
Câu 1:
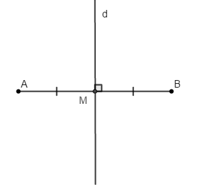
(1 điểm)
-Vẽ đoạn thẳng AB = 5cm (0,25 điểm)
-Vẽ trung điểm M của đoạn trực tiếp AB: bên trên tia AB, rước điểm M sao cho:
AM =
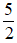
-Qua M, vẽ con đường thẳng d vuông góc cùng với AB (0,25 điểm)
Ta có: d là con đường trung trực của đoạn trực tiếp AB. (0,25 điểm)
Câu 2:
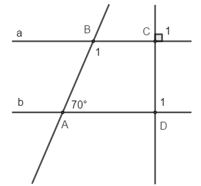
a) mang thiết, tóm lại (0,5 điểm)
| GT | 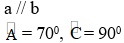 |
| KL | 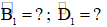 |
b,
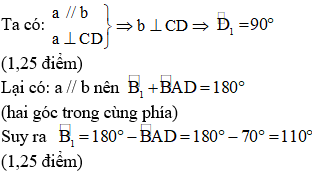
Câu 3:
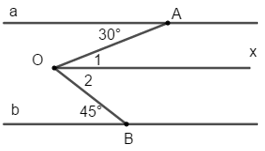
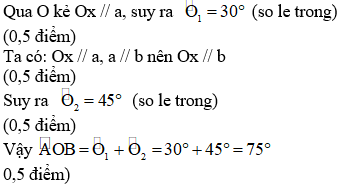
Phòng giáo dục và Đào tạo ra .....
Đề đánh giá 1 máu Chương 1 Hình học
Môn: Toán lớp 7
Thời gian có tác dụng bài: 45 phút
(Trắc nghiệm + trường đoản cú luận - Đề 3)
I. Phần trắc nghiệm khách quan (3 điểm):
Trong từng câu dưới đây, hãy lựa chọn phương án vấn đáp đúng:
Câu 1: tuyên bố nào tiếp sau đây đúng?
A. Nhị góc so le trong luôn bằng nhau.
B. Nhì góc đồng vị luôn bằng nhau.
C. Hai góc trong cùng phía luôn bù nhau
D. Hai góc đối đỉnh luôn bằng nhau.
Câu 2: hai tuyến đường thẳng không tồn tại điểm thông thường gọi là hai tuyến đường thẳng:
A. Vuông góc
B. Cắt nhau.
C. Tuy vậy song
D. Trùng nhau
Câu 3: ví như a ⊥ b và b ⊥ c thì:
A. A ⊥ c
B. A // c
C. A // b
D. C // b
Câu 4: Qua điểm A ở ở ngoài đường thẳng a, có:
A. Vô số mặt đường thẳng tuy nhiên song với a.
B. Một và có một đường thẳng tuy nhiên song cùng với a.
C. Có ít nhất một con đường thẳng song song cùng với a.
D. Hai tuyến đường thẳng tuy vậy song với a.
Câu 5: Nếu mặt đường thẳng c cắt hai tuyến phố thẳng a và b thì số cặp góc so le trong chế tạo thành là:
A. 2 cặp.
B. 3 cặp.
C. 4 cặp.
D. 5 cặp.
Câu 6: hai tuyến đường thẳng xx’, yy’ giảm nhau và trong những góc sản xuất thành gồm một góc bởi 90o, thì:
A. Xx’ là mặt đường trung trực của yy’
B. Yy’ là đường trung trực của xx’
C. Xx’ ⊥ yy’
D. Xx’ // yy’
II. Phần tự luận (7 điểm)
Câu 1: (2 điểm) Vẽ hình và viết mang thiết, kết luận của định lí (viết bằng kí hiệu):
“Một mặt đường thẳng vuông góc với 1 trong những hai đường thẳng tuy vậy song thì nó cũng vuông với mặt đường thẳng kia”.
Câu 2: (3 điểm) đến hình vẽ bên dưới đây:
a) vị sao a//b ?
b) Tính số đo của
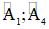
Câu 3: (2 điểm) mang lại hình vẽ. Biết: a // b, hãy tính số đo của góc AOB.
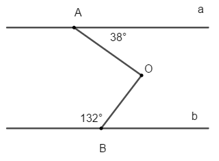
Đáp án và gợi ý làm bài
I. Phần trắc nghiệm khách quan: (3 điểm, mỗi câu đúng được 0,5 điểm).
| Câu | 1 | 2 | 3 | 4 | 5 | 6 |
| Đáp án | D | C | B | B | A | C |
Câu 1:
+ hai góc so le trong bằng nhau; hai góc đồng vị bằng nhau; nhị góc trong cùng phía bù nhau lúc có hai đường thẳng tuy nhiên song.
+ nhì góc đối đỉnh luôn bằng nhau là đúng (theo đặc điểm của nhì góc đối đỉnh).
Chọn đáp án D
Câu 2:
Hai con đường thẳng không tồn tại điểm bình thường là hai đường thẳng song song.
Chọn câu trả lời C
Câu 3:
Ta có: a ⊥ b; b ⊥ c thì a // c (quan hệ thân tính vuông góc và tính song song)
Chọn câu trả lời B
Câu 4:
Theo định đề Ơ - clít, qua điểm A ở ngoài đường thẳng a có một và có một đường thẳng song song với a.
Chọn giải đáp B
Câu 5:
Nếu mặt đường thẳng c cắt hai đường thẳng a với b thì số cặp góc so le trong tạo ra thành là 2 cặp.
Chọn giải đáp A
Câu 6:
Theo định nghĩa: hai tuyến đường thẳng xx’, yy’ giảm nhau và trong các góc tạo thành có một góc bởi 90o, thì xx’ ⊥ yy’.
Chọn giải đáp C
II. Phần từ bỏ luận: (7 điểm)
Câu 1:
- mẫu vẽ (1 điểm)
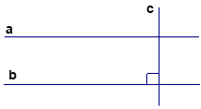
- đưa thiết, tóm lại (1 điểm)
| GT | a // b với b ⊥ c |
| KL | a ⊥ c |
Câu 2:
a) theo như hình vẽ ta có: a c; b c
Do đó: a // b (quan hệ giữa tính tuy nhiên song với tính vuông góc) (1 điểm)
b) Ta có: a // b nên:
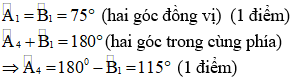
Câu 3:
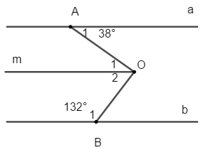
Vẽ tia Om // a (0,5 điểm)
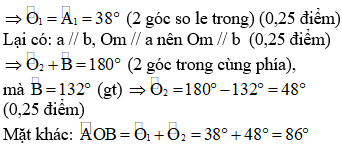
(Vì Om nằm giữa OA cùng OB) (0,75 điểm)
Phòng giáo dục và đào tạo và Đào sản xuất .....
Đề chất vấn 1 huyết Chương 1 Hình học
Môn: Toán lớp 7
Thời gian có tác dụng bài: 45 phút
(Trắc nghiệm + từ luận - Đề 4)
I. Phần trắc nghiệm một cách khách quan (2 điểm)
Câu 1: vào hình sau đây thì khẳng định nào sau đó là sai?
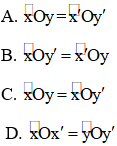
Câu 2: trong hình tiếp sau đây thì xác định nào sau đây là sai?
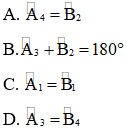
Câu 3: đến a, b, c là những đường thẳng phân biệt, xác minh nào sau đó là sai?
A. Nếu a ⊥ b cùng b // c thì a // c
B. Nếu như a // b và b // c thì a // c
C. Trường hợp a ⊥ b với b ⊥ c thì a // c
D. Nếu a ⊥ b với b // c thì
Câu 4: trong hình sau đây thì số đo góc x bằng:
A. 40o
B. 140o
C. 41o
D. 39o
II. Phần từ bỏ luận (8 điểm)
Câu 1: (7 điểm)
Cho định lý “Một con đường thẳng vuông góc với một trong các hai đường thẳng tuy vậy song thì vuông góc với con đường còn lại”.
a) chứng minh phần trả thiết, phần kết luận của định lý
b) Vẽ hình minh họa
c) Viết giả thiết, kết luận bằng kí hiệu
d) chứng tỏ ngắn gọn gàng định lý.
Câu 2: (1 điểm) Cho sau đây tìm số đo
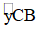
Đáp án và chỉ dẫn làm bài
I. Phần trắc nghiệm khách quan: (3 điểm, mỗi câu đúng được 0,5 điểm).
| Câu | 1 | 2 | 3 | 4 |
| Đáp án | C | D | A | A |
| Điểm | 0,5 | 0,5 | 0,5 | 0,5 |
Câu 1:
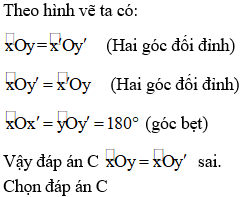
Câu 2:

Câu 3:
+) nếu như a ⊥ b cùng b // c thì a ⊥ c phải A sai, D đúng
+) giả dụ a // b cùng b // c thì a // c vừa lòng định nghĩa yêu cầu B đúng
+) giả dụ a ⊥ b với b ⊥ c thì a // c đúng theo quan hệ giới tính giữa tính song song với tính vuông góc đề nghị C đúng.
Chọn câu trả lời A
Câu 4:
Theo mẫu vẽ ta có:
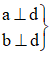
Arr; a // b
Suy ra x + 140o = 180o (hai góc trong cùng phía)
&r
Arr; x = 180o - 140o = 40o
Vậy x = 40o .
Chọn giải đáp A
II. Phần tự luận
Câu 1:
a) Phần giả thiết là: Một con đường thẳng vuông góc với một trong hai con đường thẳng tuy nhiên song (0,5 điểm)
Phần tóm lại là: vuông góc cùng với đường còn lại (0,5 điểm)
b) Vẽ hình, đặt tên (1 điểm)
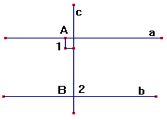
c) Viết GT, KL bằng kí hiệu (2 điểm)
| GT | c ⊥ a; a // b |
| KL | c ⊥ b |
d) vì c ⊥ a tại A cần
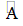
vị a // b với c giảm a tại A, c cắt b trên B buộc phải
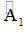
Các em học sinh lớp 7 ôn tập học kì 1 phần hình học tập với một trong những bài tập toán mà mamnongautruc.edu.vn share có giải thuật dưới đây.
Sau khi xem dứt các bài xích tập bao gồm lời giải, những em hãy từ bỏ làm bài tập ngay bên dưới để rèn luyện tài năng làm bài bác của mình. BÀI 1 :
Cho tam giác ABC. M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho BM = MD.
1. Chứng minh : ?
ABM = ?
CDM.
2. Chứng tỏ : AB // CD
3. Trên DC kéo dãn lấy điểm N làm sao để cho CD =CN (C ≠ N) minh chứng : BN // AC.
Giải.
1. Chứng minh : ?
ABM = ?
CDM.
Xét ?
ABM với CDM :
MA = MC (gt)
MB = MD (gt)

=> ?
ABM = ?
CDM (c – g – c)
2.Chứng minh : AB // CD
Ta có :

ABM = ?
CDM)
Mà :

Nên : AB // CD
3. BN // AC :
Ta tất cả : ?
ABM = ?
CDM (cmt)
=> AB = CD (cạnh tương ứng)
Mà : CD = công nhân (gt)
=> AB = CN
Xét ?
ABC với ?
NCB , ta có :
AB = cn (cmt)
BC cạnh chung.

=> ?
ABC = ?
NCB (c – g – c)
=>

Mà :

Nên : BN // AC
BÀI 2 :
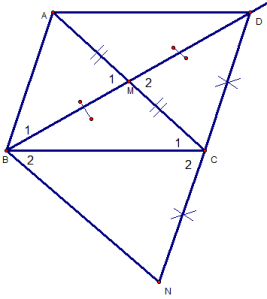
Cho tam giác ABC bao gồm AB = AC, trên cạnh AB đem điểm M, bên trên cạnh AC mang điểm N thế nào cho AM = AN. điện thoại tư vấn H là trung điểm của BC.
Chứng minh : ?ABH = ?
ACH.Gọi E là giao điểm của AH với NM. Minh chứng : ?
AME = ?
ANEChứng minh : mm // BC.
Giải.
1.?
ABH = ?
ACH
Xét ?
ABH cùng ?
ACH, ta tất cả :
AB = AC (gt)
HB = HC (gt)
AH cạnh chung.
=> ?
ABH = ?
ACH (c – c- c)
=>

2. ?
AME = ?
ANE
Xét ?
AME cùng ?
ANE, ta có :
AM =AN (gt)

AE cạnh chung
=> ?
AME = ?
ANE (c – g – c)
3. Mm // BC
Ta bao gồm : ?
ABH = ?
ACH (cmt)
=>

Mà :

=>

Hay BC

Cmtt, ta được : MN


=> mm // BC.
Bài 3 :
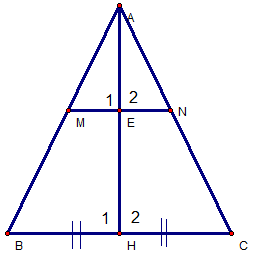
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Mang E bên trên cạnh BC làm thế nào cho BE = AB.
a) chứng tỏ : ? ABD = ? EBD.
b) Tia ED cắt tía tại M. Chứng tỏ : EC = AM
c) Nối AE. Chứng minh : góc AEC = góc EAM.
Giải.
1. ? ABD = ? EBD :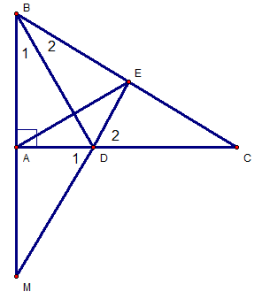
Xét ?
ABD với ?
EBD, ta có :
AB =BE (gt)

BD cạnh chung
=> ? ABD = ? EBD (c – g – c)
2. EC = AM
Ta tất cả : ? ABD = ? EBD (cmt)
Suy ra : domain authority = DE với

Xét ?
ADM cùng ?
EDC, ta bao gồm :
DA = DE (cmt)


=> ?
ADM = ?
EDC (g –c– g)
=> AM = EC.
3. 
Ta gồm : ?
ADM = ?
EDC (cmt)
Suy ra : AD = DE; MD = CD với

=> AD + DC = ED + MD
Hay AC = EM
Xét ?
AEM với ?
EAC, ta bao gồm :
AM = EC (cmt)

AC = EM (cmt)
=> ?
AEM = ?
EAC (c – g – c)
=>

BÀI 4 :
Cho tam giác ABC vuông góc trên A gồm góc B = 530.
a) Tính góc C.
b) bên trên cạnh BC, mang điểm D làm sao cho BD = BA. Tia phân giác của góc B giảm cạnh AC sống điểm E. Cmr : ΔBEA = ΔBED.
c) Qủa C, vẽ mặt đường thẳng vuông góc cùng với BE trên H. CH giảm đường trực tiếp AB tại F. Centimet : ΔBHF = ΔBHC.
d) centimet : ΔBAC = ΔBDF và D, E, F thẳng hàng.
Giải.
a. Tính góc C :
Xét ΔBAC, ta gồm :

=>

=>

b. ΔBEA = ΔBED :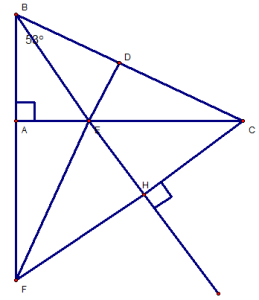
Xét ΔBEA với ΔBED, ta gồm :
BE cạnh chung.

BD = ba (gt)
=> ΔBEA = ΔBED (c – g – c)
c. ΔBHF = ΔBHC
Xét ΔBHF và ΔBHC, ta tất cả :
BH cạnh chung.


=> ΔBHF = ΔBHC (cạnh huyền – góc nhọn)
=> BF = BC (cạnh tương ứng)
d. ΔBAC = ΔBDF và D, E, F trực tiếp hàng
xét ΔBAC và ΔBDF, ta có:
BC = BF (cmt)
Góc B chung.
BA = BC (gt)
=> ΔBAC = ΔBDF
=>

Mà :

Nên :


Mặt không giống :

Mà :

Nên :


Từ (1) và (2), suy ra : DE trùng DF
Hay : D, E, F trực tiếp hàng.
===================================
BÀI TẬP RÈN LUYỆN :
BÀI 1 :
Cho ABC tất cả Â = 900. Tia phân giác BD của góc B(D ở trong AC). Bên trên cạnh BC lấy điểm E làm sao cho BE = BA.
a) đối chiếu AD cùng DE
b) triệu chứng minh:

c) chứng minh : AE

BÀI 2 :
Cho ΔABC nhọn (AB BÀI 3 :
Vẽ góc nhọn x
Ay. Bên trên tia Ax đem hai điểm B và C (B nằm trong lòng A cùng C). Trên tia Ay lấy hai điểm D và E làm sao để cho AD = AB; AE = AC
a) minh chứng BE = DC
b) hotline O là giao điểm BE cùng DC. Minh chứng tam giác OBC bởi tam giác ODE.
c) Vẽ trung điểm M của CE. Chứng minh AM là đường trung trực của CE.
Bài 4.
Cho tam giác ABC ( ABBÀI 5.
Cho tam giác ABC tất cả góc A =350 . Đường thẳng AH vuông góc cùng với BC trên H. Trên tuyến đường vuông góc cùng với BC tại B mang điểm D không thuộc nửa khía cạnh phẳng bờ BC cùng với điểm A sao để cho AH = BD.
a) minh chứng ΔAHB = ΔDBH.
b) chứng minh AB//HD.
c) gọi O là giao điểm của AD cùng BC. Chứng minh O là trung điểm của BH.
d) Tính góc acb , biết góc BDH= 350 .
Bài 6 :
Cho tam giác ABC cân tại A và bao gồm



Bài 7 :
Cho tam giác ABC cân tại A. Lấy D trực thuộc AC, E ở trong AB thế nào cho AD = AE.
Chứng minh : DB = EC.Gọi O là giao điểm của BD và EC. Chứng tỏ : tam giác OBC với ODE là tam giác cân.Chứng minh rằng : DE // BC.Bài 8 :
Cho tam giác ABC. Tia phân giác của góc C giảm AB tại D. Trên tia đối của tia CA đem điểm E làm thế nào để cho CE = CB.
Chứng minh : CD // EB.Tia phân giác của góc E cắt CD trên F. Vẽ ông xã vuông góc EF trên K. Chứng tỏ : ông xã Tia phân giác của góc ECF.Bài 9 :
Cho tam giác ABC vuông tại A có

Bài 10 :
Cho tam giác ABC (AB Đề bình chọn học kì I Môn : Toán lớp 7
Thời gian làm bài 90 phút.
BÀI 1 : (2,5 điểm) tính bằng phương pháp hợp lý :
a)

b)

c)

BÀI 2 : (2,5 điểm)
Tìm x, biết :
a)

b)

c) 33x : 11x = 81
BÀI 3 : (1,5 điểm)
Ba team cày làm việc trên ba cánh đồng có diện tích như nhau. Đội trước tiên hoàn thành quá trình trong 12 ngày. Đội vật dụng hai trả thành quá trình trong 9 ngày. Đội thứ bố hoàn thành quá trình trong 8 ngày. Hỏi từng đội có bao nhiêu vật dụng cày biết Đội đầu tiên ít hơn Đội sản phẩm công nghệ hai 2 máy và năng suất của các máy như nhau.
BÀI 4 : (3,5 điểm)
Cho tam giác ABC vuông góc trên A gồm góc B = 530.
a) Tính góc C.
b) bên trên cạnh BC, mang điểm D làm thế nào cho BD = BA. Tia phân giác của góc B cắt cạnh AC sống điểm E. Cmr : ΔBEA = ΔBED.
Xem thêm: Toán lớp 5 trang 155: ôn tập về đo thể tích, toán lớp 5 trang 155 ôn tập về đo thể tích
c) Qủa C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường trực tiếp AB tại F. Cm : ΔBHF = ΔBHC.